新式算術講義/第八章

新式算術講義
第八章
作者：高木貞治

第八章　量の連續性及無理數の起源

具體の量，抽象の量○量の原則，量の比較，加合及連續○「有理區域」，其性質，量の公約，公倍○量を計るとは何の謂ぞ○ユ—クリツドの法式，二つの場合○公約なき量の實例○ユークリツドの比の定義，比と有理數との相等及大小，二つの比の相等及大小○量と直線上の點との對照，稠密なる分布は連續に非ず，連續の定義○結論，數の原則

（一）

物の長短，輕重，明暗，冷熱，時の遲速，運動の緩急，音の高低强弱等，凡そ人の感覺に大小其度を異にする印象を與へ得べきは，皆量なり．量の特徵は其大小にあり，物の長短を考ふるに當ては，卽ち唯其長短を觀る，他の性質例へば其輕重，冷熱，色彩の濃淡等擧て之を度外に置く，又冷熱を考ふるに當ては其長短，輕重，剛柔等盡く措て問はず．斯の如くにして長短，輕重等を各〻一種の量と考ふるに至る．若し更に一步を進めて，物の如何なる性質につきて其大小を考ふるかをも顧慮せずして，卽ち，長短，輕重，冷熱につきて，唯其大小を觀て，其長さの大小，質量の大小，溫度の大小なるを問はざるときは，絕對的袖象的の量の觀念に到達す．

絕對的の量の觀念の內容は，卽ち凡ての量に普遍なる特徵の全體より成る．然れども絕對の量は抽象的にして補捉し難し，若し具象的の例證を得んと欲せば，直線の長さは就中最明亮なる印象を與ふべし．

量は之を計ることを得，量を計りたる結果は數を以て之を表はすことを得．さて量を計るとは如何，又量と數との關係は如何．

數學に於て量と稱する者旣に抽象的なり，量を計るといふことも亦理想的ならざるを得ず．實際上具象的の量を測定するは，畢竟外界が吾人の感覺に與ふる印象の强弱を定むるに外ならず．之を定むるに精粗あり，物に觸れて其冷熱を知り，音を聽きて其高低を知るは不精確なり．尺度を以て物の長さを測り，望違鏡を以て星辰の運行を觀て時刻を計るは精密なる測定なり．然れども斯の如きは測定の結果に精粗の差こそあれ，最終に訴ふる所は吾人の感覺に外ならず，卽ち觀測の方法と共に其結果の精粗異なるも，要するに是れ程度の問題にして，絕對的の精確は決して期すべからず．

實際に於ける量の測定には精確の度に限界あるを免るべからざるが故に，斯の如き測定の結果を表はすには整數のみを以て之を辨ずべし．小數を用ゐて應明上の便利を享くることあるべきも，小數點以下，假に七桁と言はんか，十桁と言はんか，若干の限りある位數以上を採るの必要なき上は，是實は整數のみを用ゐるに異ならず．

然れども實際上精密に之を測定し得べきと然らざるとを度外に置きて，理想上，各〻の量に一定不動の大さありとなすことを禁ずる能はず．數學に於て量といひ又量を計るといふは，斯の如き理想上の意義に於てしかいふなり．

（二）

吾輩の稱して量となすは，次に揭ぐる諸々の性質を具へたるものに限る．

第一，量の比較に關する原則．

一， $A$ ， $B$ なる二つの量の與へられたるとき，其間に次の三つの關係の中，いづれか一つ而も唯一つのみ成立す．

A

は

B

に等し，

A = B

A

は

B

より大なり，

A > B

A

は

B

より小なり，

A < B

等しといひ大小といふ語の意義は，よく第一章（二）及第三章（一）に揭げたる規定に遵ふべきを要す．又量の間に成立する關係は其量に代ふるに之に等しき他の量を以てせるが爲に影響を被ることなしとす．例へば $A > B$ ， $A = A^{'}$ ， $B = B^{'}$ なるとき $A^{'} > B^{'}$ なる如き是なり．

第二，量の加合に關する原則．

一， $A$ ， $B$ なる二つの量の與へられたるときは，之を加合して，一定せる第三の量 $C$ を得， $A + B = C$ ．

$C$ が一定の量なりとは， $A + B = C$ ， $A + B = C^{'}$ より $C = C^{'}$ を論斷し得べしといふに異ならず．

二，組み合はせの法則． $(A + B) + C = A + (B + C)$

三，交換の法則． $A + B = B + A$

四，加合と大小との關係． $A + B > A$ ，又 $A > A^{'}$ と共に $A + B > A^{'} + B$ ．

五，加合の轉倒． $A$ ， $B$ なる二つの量の與へられたるとき， $A > B$ ならば， $A = B + C$ なる如き量 $C$ は必ず存在す． $C = A - B$

斯の如き量 $C$ の唯一個に限り存在し得べきこと，及び $C$ の $A$ より小なるべきことは四の當然の結果なり．

倍加は加合の特例にして，量の倍加に關して第五章（四）に說きたるが如き諸事實の成立すべきこと明白なり． $A$ なる量 $n$ 個を加合して得たる量を $A$ の $n$ 倍といひ，之を表はすに $n A$ なる記號を以てす．

第三，連續の原則

量は連續の性質を具ふ．

量に連續ありとは，量の變動（卽ち其增減）の連續的なるを得るをいふ．物の數の變動の少くとも一個を下ることを得ざるが如きは卽ち變動の連續的ならざるなり，之に反して，例へば長さ，時間の如き所謂量にありては其變動連續的なるを得ること何人も承認する所なり．然れども連續といふことを最明白に言ひ表はすことは甚だ難きが故に，其說明は之を後條に讓り，此處には姑らく量の連續に關せる二三の事實を列記するに止むべし．

アルキメデスの法則． $A$ , $B$ なる量與へられ， $A$ は $B$ より大なるとき， $B$ を幾囘も加合し行きて，竟に $A$ より大なる量に到達すべし，卽ち $B$ の倍の中に必ず $A$ より大なる者あり， $n B > A$ なる如き自然數 $n$ 必ず存在す．

等分の可能．凡て量は之を任意の相等しき部分に分ち得べし，卽ち $A$ なる量と $n$ なる自然數の與へられたるとき $A = n B$ なる如き量 $B$ は必ず存在す． $B$ を $A$ の $n$ 分の一と名づけ，之を表はすに $\frac{A}{n}$ なる記法を以てす． $B$ の如き量は唯一個に限り存在し得べきこと勿論なり．

稠密なる分布． $A$ ， $B$ が相異なる量ならば $A$ ， $B$ の中間に必ず第三の量 $m$ を容る，隨て $A$ ， $B$ の中間には無限に多くの量存在す．

此事實は前條の當然の結果なり．今 $A$ を $B$ より大なりとせば，第二原則五によりて $C = A - B$ なる如き量 $C$ は必ず存在す．さて等分の可能に基き $\frac{C}{2}$ なる量は必ず存在し， $B + \frac{C}{2}$ は $A$ ， $B$ の中間にあり， $A > B + \frac{C}{2} > B$ ．量に最大の者なく，又最小の者なし．げにも $A$ を如何なる量なりとするも $2 A$ は $A$ よりも大にして又 $\frac{A}{2}$ は $A$ よりも小なり．

以上列擧せるはいづれも量の連續に關せる性質なり．然れどもこれら未だ連續といふことの特徵を盡すに足らざること，後文に至て自ら明なるべし．

（三）

量の倍加及等分に關して第五章（四）に說ける如き諸定理成立す，これらの諸定理はいづれも極めて明白にして，殆んど辯說を要せず．此處に記法の說明として唯一つの事實を擧ぐべし．

$A$ を一の量とし， $m$ ， $n$ を自然數となすときは $\frac{m A}{n}$ は $A$ の $m$ 倍 $m A$ の $n$ 分の一を，又 $m (\frac{A}{n})$ は $A$ の $n$ 分の一の $m$ 倍を表はし，兩者相等しきこと容易に證明せられ得べし．此相等しき量を表はすに

\frac{m}{n} A

なる記法を以てす．又は $\frac{m}{n}$ なる分數を一個の文字例へば $r$ にて示せるときは，更に之を畧して

r A

と記すべし．此處なほ讀者の注意を乞ふべき一條あり．こゝに $A$ ， $B$ の如き文字を以て量を表はせること是なり．卽ち此等は量の數値を表はせるに非ずして直に量其者を代表せるなり．例へば $A$ を以て圖の第一の直線（長さ）を表はせりとせば $2 A$ は第二， $\frac{2}{3} A$ は第三の直線を表はせり． $A$ の幾寸，幾インチ，幾センチメートルなるかは問ふ所に非ず，否， $A$ は若干寸，若干インチなりとは如何なる意義を有するかは，吾人の之より進みて知らんと欲する所なり．

$E$ なる量の與へられたる時， $r$ を正の有理數（自然數及び正の分數）となし $r E$ の如き量，卽ち $E$ より倍加及び等分によりて作り得べき量を總て一括し，假に之を有理區域と名づけ，此有理區域は $E$ なる量によりて定められたりと稱す．

$E$ の定むる有理區域に屬せる二個の量 $r E$ ， $r^{'} E$ の和又は差は $(r \pm r^{'}) E$ にして，此量は又同一の有理區域に屬せり．又 $n$ を自然數とせば $\frac{r E}{n} = \frac{r}{n} E$ 卽ち或有理區域に屬せる量に加合（及び倍加）等分を施こせる結果は亦同一の有理區域に屬せる量なり．

$E$ の定むる有理區域に屬せる量の一つを $E^{'}$ と名づけ $E^{'} = c^{'} E$ と置く， $c^{'}$ は自然數又は正の分數なり．さて一般に $r$ を以て正の有理數を表はすときは（三）によりて

r E^{'} = r c^{'} E, r E = \frac{r}{c^{'}} E^{'}

にして $\frac{r}{c^{'}}$ は勿論正の有理數なるが故に $E$ の有理區域に屬せる量は必ず亦 $E$ の有理區域に屬す．此等の關係は $E$ ， $E^{'}$ の同一の有理區域を定むるを示せり．語を換へて之を言はゞ，凡て有理區域は之に屬せる唯一つの量によりて全く定まるなり．

$A_{1}$ ， $A_{2}$ が同一の有理區域（例へば $E$ の定むる有理區域）に屬せる量ならば

A_{1} = \frac{m_{1}}{n_{1}} E, A_{2} = \frac{m_{2}}{n_{2}} E

なるにより

m_{2} n_{1} A_{1} = m_{1} n_{2} A_{2} = m_{1} m_{2} E

$m_{2} n_{1}$ ， $m_{1} n_{2}$ なる二つの自然數が相素ならずば之を其最大公約數にて除し

a_{2} A_{1} = a_{1} A_{2}

なる如き相素なる自然敷 $a_{1}$ ， $a_{2}$ の必ず存在すべきを知る．此相等しき量を $M$ と名づくれば $M$ は $A_{1}$ 及び $A_{2}$ の倍量，卽ち $A_{1}$ ， $A_{2}$ の公倍量にして，而も $A_{1}$ ， $A_{2}$ の公倍量の中最小なる者なり． $M$ を $A_{1}$ ， $A_{2}$ の最小公倍量といふ．上の關係より

\frac{A_{1}}{a_{1}} = \frac{A_{2}}{a_{2}}

を得，之を $D$ と置かば $D$ は $A_{1}$ ， $A_{2}$ の最大公約量なり．最大公約量といふ語の意義は說明を須ひずして明瞭なるべし． $M$ と $D$ との間には次の關係成立す．

M = a_{1} a_{2} D .

$A_{1}$ ， $A_{2}$ の公倍量は凡て $M$ の倍量にして， $A_{1}$ ， $A_{2}$ の公約量は凡て $D$ の約量なり．又 $D$ の約量は盡く $A_{1}$ ， $A_{2}$ の公約量なるが故に， $A_{1}$ ， $A_{2}$ には限りなく多くの公約量存在せり．

以上の觀察によりて次の結果に到達す．

公倍ある二量には公約あり，又公約ある二量には必ず公倍あり．公約ある二量は唯一つの最大公約及び無限に多くの公約を有す．同一の有理區域に屬せる二つの量には必ず公約あり，公約を有せる二つの量は必ず同一の有理區域（例へば此公約の定むる有理區域）に屬す．有理區域は二つづつ互に公約を有する凡ての量の集合なり．

（四）

量を計るといふことは前に述べたる量の原則を基礎とす． $A$ なる量の與へられたるとき，一定の量 $E$ を採りて之を單位となし， $E$ を倍加して

(1)

E, 2 E, 3 E, \dots n E, \dots

等の量を作り，之を $A$ と比較するに， $A$ が此等の量の中の一つに等しく，例へば $A = n E$ なるときは， $n$ は卽ち $E$ を單位としての $A$ の數値なり． $A$ 若し $E$ の倍に等しからずば，アルキメデスの法則によりて， $E$ の倍にして $A$ よりも大なるもの必ず存在す，隨て (1) の量の中 $A$ より大ならざるものは其數限りあり．故に其中に一個最大の者なかるべからず．今 $n E$ を以て (1) の量の中 $A$ を超えざる最大の者となさば

(2)

(n + 1) E > A > n E

にして，此場合に於ては， $A$ の數値は $n$ より大にして $n + 1$ より小なりといふ，若し

A - n E = R

と置かば

A = n E + R, R < E

卽ち $A$ と數値 $n$ なる量との差 $R$ は $E$ より小なり．斯の如くにして $E$ を單位として， $A$ を $E$ の程度まで計ることを得．

若し更に $t$ を $1$ より大なる自然數とし，

E^{'} = \frac{E}{t}

と置き， $E$ に代ふるに $E^{'}$ を以てして，同樣の手續きを反復し，例へば

(1*)

A = m E^{'} = \frac{m}{t} E

なる結果に到達したるときは $E$ を單位としての $A$ の數値は $\frac{m}{t}$ なり，或は又 (2) に於ける如く

(m + 1) E^{'} > A > m E^{'}

ならば

(2*)

\frac{m + 1}{t} E > A > \frac{m}{t} E

にして， $A$ の數値は $\frac{m}{t}$ より大にして， $\frac{m + 1}{t}$ より小なり，若し

A - m E^{'} = R^{'}

と置かば

A = \frac{m}{t} E + R^{'}, R^{'} < \frac{E}{t}

にして，斯の如くにして $A$ を $\frac{E}{t}$ の程度まで計ることを得たり．

今任意に $D$ なる量を與ふるときは，アルキメデスの法則によりて

D > \frac{E}{t}

なる如き自然數 $t$ は必ず存在す．斯の如く $t$ を定めたる後 (1*) 又は (2*) によりて $m$ を定むるとき

A = \frac{m}{t} E + R, R < \frac{E}{t}

より

R < D

を得， $D$ の程度まで $A$ を計ることを得．

是に由りて考ふるに， $A$ を計るとは $E$ なる單位を定め， $E$ の定むる有理區域に屬せる量

\frac{m}{t} E

と $A$ とを比較するに外ならず． $A$ 若し此有理區域に屬せば，卽ち若し

A = \frac{m}{t} E

なる如き量 $\frac{m}{t} E$ 存在せば， $\frac{m}{t}$ を $A$ の數値となす．單位 $E$ と數値 $\frac{m}{t}$ との與へられたるとき， $A$ なる量は一定なり．若し又 $A$ が此有理區域に屬せざるときは，如何程小なる量 $D$ を豫め定むるとも

A - \frac{m}{t} E < D

又は

\frac{m}{t} E - A < D

なる如き量 $\frac{m}{t} E$ は必ず存在す．然れども此場合には $A$ の數値は $\frac{m}{t}$ より大，又は $\frac{m}{t}$ より小なり． $E$ と $\frac{m}{t}$ との與へられたるとき，上の如き條件に適合すべき量 $A$ は限りなく多く存在せり． $A$ は未だ $E$ 及び $\frac{m}{t}$ と共に一定せりと言ふことを得ず．

玆に於てか次の疑問を生ず， $E$ なる定まりたる量より倍加及び等分によりて作り得べき量の範圍卽ち所謂 $E$ の有理區域は果してよく凡ての量を包括するか，或は又此範圍に含蓄せられざる量は實際存在すべきか．又若し此の如き量にして存在せば，其數値は如何．

（五）

ユークリツドは二つの量の公約を定むる方法を敎ふ．此方法は現代の數學に於ても甚重要なる者にして，ユークリツドの法式の名を以て汎く知られたり．

先づ $A_{1}$ ， $A_{2}$ なる二つの量を與ふ，此中の一方例へば $A_{1}$ が他の一方 $A_{2}$ の倍量なる場合（ $A_{1} = A_{2}$ を含む）は最簡單にして辨明を要せず． $A_{1}$ 若し $A_{2}$ より大にして，而も $A_{2}$ の倍量ならずば，（四）に於て說きたる如くにして

A_{1} = n_{1} A_{2} + A_{3}, A_{3} < A_{2}

なる如き自然數 $n_{1}$ 及び $A_{3}$ なる量を定むることを得， $A_{2}$ ， $A_{3}$ につきて同樣の手續きを行ひ

A_{2} = n_{2} A_{3} + A_{4}, A_{4} < A_{3}

を得，次第に斯の如くにして，一般に

(1)

A_{k} = n_{k} A_{k + 1} + A_{k + 2}, A_{k + 2} < A_{k + 1}

を得． $A_{1}$ ， $A_{2}$ より順次減少する一定の量の引續き $A_{3}, A_{4}, A_{5}, \dots$ を作る．

さて玆に二つの場合を區別すべし．

第一，此手續きを繼續すること若干囘にして

(2)

A_{h - 1} = n_{h - 1} A_{h}

の如き關係竟に一度は成立し，ユークリツドの法式こゝに其終局に達するときは， $A_{1}$ ， $A_{2}$ は公約を有し， $A_{h}$ は卽ち其最大公約量なり．

實にも，先づ (2) によりて $A_{h}$ は $A_{h - 1}$ の約量なり，次に (2) に先てる

A_{h - 2} = n_{h - 2} A_{h - 1} + A_{h}

より

A_{h - 2} = (n_{h - 2} n_{h - 1} + 1) A_{h}

を得， $A_{h}$ の亦 $A_{h - 2}$ の約量なるを知る，次第に斯の如く遡り行きて竟に $A_{h}$ は $\dots A_{3}, A_{2}, A_{1}$ の約量なるを知る， $A_{h}$ は $A_{1}$ ， $A_{2}$ の公約量なり．

是故に $A_{1}$ ， $A_{2}$ には公約量あり，其一つを $D$ と名づくれば $D$ は亦 $A_{3}$ の約量，隨て又 $A_{1}, A_{2} \dots A_{h}$ の約量なり． $A_{h}$ は $A_{1}$ ， $A_{2}$ の公約量にして， $A_{1}$ ， $A_{2}$ の公約量は必ず $A_{h}$ の約量なり．是 $A_{h}$ が $A_{1}$ ， $A_{2}$ の最大公約量なるを示せるに非ずして何ぞや．

第二の場合は，ユークリツドの法式の決して終局に達することなき，是なり．

さて

A_{k} = n_{k} A_{k + 1} + A_{k + 2}, A_{k + 1} > A_{k + 2}

にして，又 $A_{k} > A_{k + 1}$ 隨て $n_{k} ≧ 1$ ， $n_{k} A_{k + 1} > A_{k + 2}$ なるにより

A_{k} > 2 A_{k + 2}

是故に

A_{1} > 2 A_{3}, A_{3} > 2 A_{5}, A_{5} > 2 A_{7}, \dots A_{2 h - 1} > 2 A_{2 h + 1}

隨て

(3)

A_{1} > 2^{h} A_{2 h + 1}, A_{2 h + 1} < \frac{A_{1}}{2^{h}}

又同樣にして

(3)

A_{2 h + 2} < \frac{A_{2}}{2^{h}}

或は $A_{1} > A_{2}$ なるにより， $A_{2 h + 1}$ 及び $A_{2 h + 2}$ は共に $\frac{A_{2}}{2^{h}}$ より小なり．

是によりて $A_{1}, A_{2}, A_{3}, A_{4} \dots$ は順次減少して，究まる所なし． $K$ を如何に小なる量なりとするも， $A_{n}$ は附數 $n$ の增大するとき，竟に $K$ よりも尙小となるべし．其故如何にといふに，先づ

(4)

A_{2} < g K, K > \frac{A_{2}}{g}

なる如き自然數 $g$ はアルキメデスの法則によりて必ず存在す．さて，指數 $m$ を相當に採りて

(5)

2^{m} > g

となすことを得，例へば $2$ を命數法の基數として $g$ を展開するとき， $g$ の桁數，若干，此桁數を $m$ とせば第二章（七）によりて上の不等式は成立すべし．

$K$ の與へられたるとき (4) に從て $g$ を定め，次に (5) に從て $m$ を定むれば

K > \frac{A_{2}}{g} > \frac{A_{2}}{2^{m}}

よりて (3) によりて

K > A_{2 m + 1}, A_{2 m + 2}

$A_{2 m + 1}, A_{2 m + 2}$ は果して $K$ よりも小なり．

斯の如く $A_{1}, A_{2}, A_{3} \dots$ は漸次減少して究まる所なきが故に，此第二の場合に於ては $A_{1}$ ， $A_{2}$ に公約あるを得ず．げにも假に $A_{1}$ ， $A_{2}$ に公約ありとせば，其一を $D$ と名づけんに， $D$ は亦 $A_{3}, A_{4} \dots$ の約量ならざるを得ず，而も $A_{3}, A_{4} \dots$ は漸次咸少して竟に如何なる量よりも，隨て $D$ よりも小となるべきが故に，是不可有の事に屬せり．

$A_{1}$ ， $A_{2}$ に公約あるときはユークリツドの法式は其終局に於て $A_{1}$ ， $A_{2}$ の最大公約量を與ふ，ユークリツドの法式終局に達せざるときは $A_{1}$ ， $A_{2}$ に公約あることなし．然りと雖，實際に於て $A_{1}$ ， $A_{2}$ なる二つの量，例へば二つの直線の與へられたる時，此方法を利用して其公約の存否を決定することを得ず．何とならば $A_{1}$ ， $A_{2}$ に上述の手續きを適用すること若干囘にして未だ終局に達せざりしとするも，其竟に終局に達すべきや否やは，之によりて決定すべからざればなり．凡ての場合に於て，公約の存否を決定して誤る所なき方法は吾人未だ之あるを知らず．

（六）

公約なき二つの量は存在すべきかとの疑問の解決竟に如何．ユークリツドの法式は公約ある場合に，最大公約を與ふ，ユークリツドの法式終局に達せざるを確め得ば，公約の存在せざるを知るべしと雖，ユークリツドの法式は其自身の竟に終結すべきや否やを敎ふるものにあらざるを奈何せん．

ユークリツドの法式の根據は（二）に述べたる量の原則にあり．今飜て此原則を吟味せば，此原則が公約なき二量の存否を決定するに足らざるを悟らん．

一有理區域以外に量あるや否やは姑らく措きて，一有理區域の量のみに着眼して，之を一系統となすに，此系統はよく（二）の諸原則に適合せり．（二）の諸原則に於て「量」といへる語に代ふるに「一有理區域の量」といふを以てするとき，此等の諸原則は盡く實現せらるべし．有理區域內の二量必ず比較し得べく，其加合は常に同一有理區域內に於て可能にして，連續に關する三つの性質も亦一有理區域內の量のみにつきて旣に成立す．

夫れ，一有理區域の量のみを以てして旣に（二）の諸原則を充實すべし．卽ち一有理區域以外に量あると然らざるとは（二）の原則の與り知らざる所なり．公約なき二量の存否を決定すべき所以の者は此等の原則以外に之を求めざるべからず．

公約なき二量の實例は之をユークリツド幾何學より學び得べし．平方形の一邊と其對角線とは公約なき二つの長さなりといへるは，ユークリツドの諸定理の中最有名なる者の一なり．

此有名なる定理の證明を此處に反復すること，決して其所を得ざる者と謂ふべからず．此定理はユークリツドの法式に終結あるを確知し得べき，特別の場合としても亦注意に値す．

$a b$ を一邊とせる平方形の對角線 $a c$ の上に於て $a b = a b^{'}$ なる點 $b^{'}$ を定め， $b^{'}$ より $a c$ に垂直に $b^{'} d$ を引きて， $d$ に於て $b c$ を切らしむ．

A_{1} = a c A_{2} = a b

と置かんに，先づ $A_{1} > A_{2}$ さて三角形の二邊の和は他の一邊よりも大なるが故に

a c < a b + b c = 2 \cdot a b

卽ち

A_{1} < 2 A_{2}

よりて

n_{1} = 1, A_{1} = A_{2} + A_{3}, A_{3} = c b^{'}

A_{2} = c b = d b + c d

$c$ 及び $d$ にて標ある二つの角は共に半直角なるが故に $c b^{'} = b^{'} d$ 又 $b$ 及び $b^{'}$ にて標ある二つの角は相等しきが故に $b^{'} d = d b$ よりて $d b = c b^{'} = A_{3}$

さて $c d$ は $A_{3}$ を一邊とせる平方形の對角線なるが故に

2 A_{3} > c d > A_{3}

よりて

3 A_{3} > A_{2} = c d + A_{3} > 2 A_{3}

A_{2} = 2 A_{3} + A_{4}

$A_{3}$ を一邊とせる平方形に於て $A_{1}$ は， $A_{2}$ を一邊とせる平方形に於ける $A_{3}$ と同樣の位置にあるが故に， $A_{3}$ ， $A_{4}$ につきて同樣の論法を反復し

A_{3} = 2 A_{4} + A_{5}

を得，次第に斯の如くにして，此場合に於てはユークリツドの法式の終局に達することなきを推知すべし．

此結果は又次の如くにして之を說明することを得．先づ $E$ を一邊とせる平方形の對角線を $E^{'}$ とせば， $E^{'}$ を一邊とせる平方形の對角線は， $2 E$ なること圖を一見して明瞭なり．假に $E^{'}$ は $E$ の有理區域に屬せりとなし，例へば $E^{'} = r E$ なりとせば，又 $2 E = r E^{'}$ ならざるを得ず．故に $2 E = r r E$ 隨て

2 = r r

を得．さて斯の如き有理數 $r$ の存在せざることは次の如くにして之を證明すべし．假に斯の如き有理數存在すとし，之を旣約分數となして $\frac{p}{q}$ を得たりとせば $p^{2} = 2 q^{2}$ 卽ち $2 q^{2}$ は $p$ の倍數ならざるを得ず，而も $q$ 隨て又 $q^{2}$ は $p$ と素なるが故に $p$ は $2$ の約數卽ち $1$ 又は $2$ なり．さて $p$ は $1$ なることを得ざることは明なり．若し $p$ を $2$ なりとせば $2 = q^{2}$ にして如何なる整數の平方も $2$ に等しきを得ず．是故に $p^{2} = 2$ なる如き有理數 $r$ は存在することなし．

（七）

ユークリツドの比例論は數の觀念の歷史の第一頁を飾りて特に異彩を放つ．讀者は，其嘗て初等幾何學の一節として相識れる此理論に，算術を榜標せる本書に於て再び邂逅するに驚くことなかるべし．

此處にエレメンツの字句を忠實に反復するの必要なし，吾輩はユークリツドの比の定義を次の如く言ひ表はさんとす．

第一定義． $A$ ， $B$ なる二つの量の與へられたるとき， $m$ ， $n$ を二つの自然數となし， $n A$ 及び $m B$ を比較して三つの場合を區別す，一に日く， $n A$ は $m B$ に等し，二，三に曰く $n A$ は $m B$ よりも大又は小なり．或は之を換言して，一に曰く $\frac{A}{m}$ は $\frac{B}{n}$ に等し，二，三に曰く $\frac{A}{m}$ は $\frac{B}{n}$ よりも大又は小なり．此三つが凡ての場合を網羅せることは（二）の第一原則の保證する所なり．さて第一の場合に於ては $A$ ， $B$ の此 $A : B$ は有理數 $\frac{m}{n}$ に等しといひ，第二，第三の場合に於ては $A : B$ は $\frac{m}{n}$ よりも大又は小なりといふ．卽ち

n A ≷ m B

卽ち

\frac{A}{m} ≷ \frac{B}{n}

と共に

A : B ≷ \frac{m}{n}

例へば $A$ を $B$ を一邊とせる平方形の對角線となすとき， $m$ ， $n$ を $1$ ， $2$ となさば $A < 2 B$ なるが故に

A : B < 2

又 $m$ ， $n$ を $2$ ， $1$ となさば $2 A > B$ なるが故に $A : B > \frac{1}{2}$

第一定義は $A : B$ なる者に，有理數に對する大小の順序に於て一定の位置を與ふ． $A : B$ なる者には本來定まれる意義あるにあらずして，吾輩のユークリツドと與に今新に其意義を定めんとするものなるが故に， $A : B$ と有理數との大小の關係は自家撞着に陷らざる限り，隨意に之を定めて不可あることなし．然れども大小相等の語には旣に慣用の意義あるが故に，此意義に協はざる凡ての新定義は無益にして有害なり．玆に於て次の三點につきて，上文の第一定義を詮衡するの必要を生ず．

\frac{m}{n} = \frac{m^{'}}{n^{'}}

なるとき

A : B = \frac{m}{n}

と同時に

A : B = \frac{m^{'}}{n^{'}}

なりや，

\frac{m}{n} > \frac{m^{'}}{n^{'}}

なるとき

A : B > \frac{m}{n}

と同時に

A : B > \frac{m^{'}}{n^{'}}

なりや，

\frac{m}{n} < \frac{m^{'}}{n^{'}}

なるとき

A : B < \frac{m}{n}

と同時に

A : B < \frac{m^{'}}{n^{'}}

なりや，

第一， $\frac{m}{n} = \frac{m^{'}}{n^{'}}$ ， $A : B = \frac{m}{n}$ より $m n^{'} = m^{'} n$ ； $n A = m B$ を得，隨て $m n^{'} (n A) = m^{'} n (m B)$ 卽ち $m n (n^{'} A) = m n (m^{'} B)$ よりて $n^{'} A = m^{'} B$ 故に果して $A : B = \frac{m^{'}}{n^{'}}$ 第二，第三類推すべし．

$A$ ， $B$ に公約あるときは，第一定義によりて $A : B$ は或有理數 $r$ に等しく，（三）に說ける意義に隨て $A = r B$ ．又若し $A$ が $B$ の有理區域に屬し $A = r B$ なる如き有理數 $r$ にして存在せば，第一定義に從ひて $A : B$ は此有理數 $r$ に等し．これ當然にして無奇なる事實なり．

然れどもユークリツドは旣に公約なき二つの量の存在するを知れり． $A$ ， $B$ に公約なきときは $A : B$ の比は如何．此場合にありては $m$ ， $n$ を如何なる自然數となすとも $n A = m B$ なること，卽ち $r = \frac{m}{n}$ を如何なる有理數となすとも $A : B = r$ なること決してあり得べからざるにより， $A : B$ は或は $r$ より大に或は $r$ より小なり．是故に $A : B$ より小なる有理數を盡く甲の群に編入し，又 $A : B$ より大なる有理數を盡く乙の群に編入して，凡ての有理數を兩分することを得．斯の如くにして $A : B$ より生出する有理數內の切斷は次の三條件を充實せり．

一，凡ての有理數（勿論正の有理數，以下同じ）は必ず甲乙二群の中いづれか一方に，而も唯一方にのみ，屬す．

二，甲に屬する有理數は凡て乙に屬する有理數より小なり．

三，甲に屬する有理數の中に最大の者なく，乙に屬する有理數に最小の者なし．

第三の外は辨明を要せざるべし，甲に屬せる有理數の中任意に一個を採りて之を $r_{0}$ と名づくれば $A : B > r_{0}$ 卽ち $A > r_{0} B$ さて $A - r_{0} B$ と $B$ とにアルキメデスの法則を適用して $A - r_{0} B > \frac{B}{p}$ なる如き自然數 $p$ の存在すべきを知る．卽ち $A > (r_{0} + \frac{1}{p}) B$ ， $A : B > r_{0} + \frac{1}{p}$ にして $r_{0} + \frac{1}{p}$ なる有理數は $r_{0}$ より大にして而も仍ほ甲に屬せり．是によりて甲の有理數に最大の者あるを得ざるを知るべし．乙に屬せる有理數の中に最小の者あるを得ざること，亦同樣にして證明せらるべし．

斯の如くにして有理數の範圍に尙ほ缺陷あるを知り得たり，有各處稠密なりと雖，其中に公約なき二量の比 $A : B$ を以て塡充空隙を存せり．

凡ての比と凡ての有理數との大小相等の關係は第一定義によりて旣に定まれり，今二つの比の相等及び大小の意義を定めんが爲に，ユークリツドと共に次の定義を立す．

第二定義 $A : B$ ， $A^{'} : B^{'}$ 共に有理數に等しからば，此等の有理數の相等大小によりて比の相等大小を定む．二つの比の中一方例へば $A^{'} : B^{'}$ のみが有理數 $r^{'}$ に等しからば $A : B$ と $r^{'}$ との相等大小によりて，兩比の相等大小を決す．二つの比がいづれも有理數に等しからずば，此等の比の與ふる有理數切斷の結果を比較すべし．甲，乙の語に代ふるに $𝐔$ ， $𝐎$ を以てし， $A : B$ より大又は小なる有理數の全體をそれぞれ $𝐎$ ， $𝐔$ 又 $A^{'} : B^{'}$ より大又は小なる有理數との全體をそれぞれ $𝐎^{'}$ ， $𝐔^{'}$ と名づく．

さてこゝに三つの場合あり．

（一） $A : B$ ， $A^{'} : B^{'}$ は同一の切斷を與ふ，卽ち $𝐎$ ， $𝐎^{'}$ 隨て又 $𝐔$ ， $𝐔^{'}$ は全く同一の有理數より成る．此場合には $A : B$ と $A^{'} : B^{'}$ とを相等しとなす．

$A : B$ と $A^{'} : B^{'}$ とが同一の切斷を與へざるときは， $𝐎$ ， $𝐎^{'}$ 隨て又 $𝐔$ ， $𝐔^{'}$ は相異なり．

（二） $𝐎$ は $𝐎^{'}$ に屬せざる有理數（ $r$ ）を含む．此場合には $𝐎^{'}$ に屬せる有理數は盡く $𝐎$ に屬せり．げにも， $r$ は $𝐎^{'}$ に屬せず，隨て $r$ は $𝐔^{'}$ に屬せるが故に， $𝐎^{'}$ の有理數は盡く $r$ より大なり，さて $r$ は旣に $𝐎$ に屬せるが故に， $r$ より大なる有理數は盡く $𝐎$ に屬せり．是故に $𝐔^{'}$ は $𝐔$ に屬せざる有理數（ $r$ ）を含み， $𝐔$ に屬せる有理數は盡く $𝐔^{'}$ に屬す． $A^{'} : B^{'} > r > A : B$

（三） $𝐎^{'}$ は $𝐎$ に屬せざる有理數（ $r^{'}$ ）を含む．此場合には $𝐎$ は $𝐎^{'}$ の一部分， $𝐔^{'}$ は $𝐔$ の一部分にして $A : B > r^{'} > A^{'} : B^{'}$

（二）の場合には $A : B$ を $A^{'} : B^{'}$ より小となし，（三）の場合には $A : B$ を $A^{'} : B^{'}$ より大となす．

（一），（二），（三）は凡ての場合を網羅せり，此等の場合に於ける有理數兩斷の狀況は次の圖によりて說明せらるべし

（一）
（二）
（三）

こゝに定めたる大小相等の意義につきても，亦次の諸點を審査せざるべからず．

$A : B = A^{'} : B^{'}$ ， $A : B = A^{″} : B^{″}$ と同時に $A^{'} : B^{'} = A^{″} : B^{″}$ なりや，

$A : B > A^{'} : B^{'}$ ， $A : B > A^{″} : B^{″}$ と同時に $A^{'} : B^{'} > A^{″} : B^{″}$ なりや，

$A : B < A^{'} : B^{'}$ ， $A : B < A^{″} : B^{″}$ と同時に $A^{'} : B^{'} < A^{″} : B^{″}$ なりや，

或は此最後の一問に代ふるに次のを以てすべし，

$A : B > A^{'} : B^{'}$ と同時に $A^{'} : B^{'} < A : B$ なりや，

例へば第二の問に答へんとするに，先づ $A : B > A^{'} : B^{'}$ なりといふは $A : B > r > A^{'} : B^{'}$ なる如き有理數 $r$ の存在するをいふに外ならず，又 $A^{'} : B^{'} > A^{″} : B^{″}$ は $A^{'} : B^{'} > r^{'} > A^{″} : B^{″}$ なる如き有理數 $r^{'}$ の存在を保證す．さて $r > A^{'} : B^{'}$ ， $A^{'} : B^{'} > r^{'}$ より $r > r^{'}$ を知り $A : B > r$ ， $r > r^{'}$ より，第一定義によりて $A : B > r^{'}$ を知る，之を $r^{'} > A^{″} : B^{″}$ と倂せ考へて果して $A : B > A^{″} : B^{″}$ なるを確む．其他類推すべし．

斯の如くにして凡ての場合に於て二つの比の相等，大小を定むることを得たり．

$A$ ， $B$ が公約なき場合に於ける $A : B$ なる比の値は，卽ち吾輩のこれより說明せんとする無理數に外ならず．ユークリツドの比の定義より無理數の觀念に到達するは，實に一擧手一投足のみ．ユークリツドの比例論は實質に於て，現代數學に於ける數の觀念の凡ての要素を具へたり．數の觀念の完成とユークリツド比例論との間に，歷史が二千載の空隙を示せること，今にして之を想へば，實に奇異なりと謂ふべし．事實を知るは易し，其價値を批判するは難し．要は唯立脚點の昂上にあり．

（八）

（二）に擧げたる原則の未だ量の特性を盡さゞるを指摘せる後，而して此缺陷を補修するに先ち，前節に於て古希臘時代に於ける比の觀念を囘顧したるは，以て現時に於ける數の觀念の由る所を明にせんと欲せるに外ならず．

吾人の所謂量に連續の性質あり，而して（二）に擧げたる量の連續に關する性質は，未だ其特徵を盡くさず，此缺陷は何處にか伏在せる．

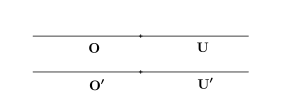
抽象的の量を表はすに，直線の長短を以てし，更に一層明瞭なる形象を得んが爲に，長さを直線上の點に對照せんとす． $O$ なる點に始まりて，限りなく一方に延長せる直線を考へ，或る一定の長さ $A$ を採り， $O P$ を此長さに等しくして， $P$ 點を定め，以て $A$ なる長さを， $P$ なる點に對照す．斯の如くにして個々の長さと此直線上の個々の點とを配合するときは，各の長さは或る定まりたる點によりて表はされ，又各の點は或る定まりたる長さを表はし且つ長さの大小は之を表はせる點の位置の左右によりて定まる．量に連續の性質ありといふは，直線上の點は連續せりといふに異ならず．直線上の點連續せりといふことは，明確にして動かすべからざるの觀ありと雖，さて此連續といへる觀念を分析して，之を最も明白なる言辭に表はさんことは甚だ難し．

直線上に於て，例へば $P$ より $Q$ に移らんとするときは $P$ ， $Q$ の中間の諸點を盡く通過せざるべからず，此等の點は $P$ より $Q$ に達すべき徑路を組成し，其間何處にも斷絕あることなし．分布の稠密といふことは，畢竟如何なる二點の中間にも限りなく多くの點あるべきを明言するものなれば，此原則は一見點の連續を表明して餘蘊なきが如し．然れども其實際然らざるを覺ること容易なり．

今直線上隨意の一點を除き去りたりとせよ，譬へば，理想的最銳利のナイフを以て， $D$ に於て此直線を切りたりとせよ，卽ち此切り目に幅なしと考へよ，斯の如くにして直線上點の連續は破壞せらる．然れども如何なる二點の中間にも必ず第三の點あるべしとの條件は， $D$ を除去せる後にも，仍ほ依然として充實せらるゝにあらずや．是分布の稠密は未だ連續といふことの特徵たるに足らざるを證する者なり．

連續の觀念明白なるが如くにして，實は然らず．此微妙なる觀念を捕捉して，之に蔽ふ所なき光明を與へたるはデヾキンドの功績に歸す．デヾキンドは連續の定義を定めて曰く，

直線上の凡ての點を甲乙の二群に分ち，甲の群の點をして盡く乙の群の點の左方に在らしむるとき，直線を斯の如く兩分する點は必ず，而も唯一個に限り存在す．

卽ちこゝに謂ふ所の線の兩斷は次の性質を具へたり．

一，直線上の凡ての點は必ず甲又は乙の中いづれか一方，而も唯一方にのみ，屬す．

二，甲に屬する點は盡く乙に屬する點の左方にあり．

三，斯の如くするときは甲に屬する點の中最右に位する者唯一個あるか，或は乙に屬する點の中最左に位する者，唯一個あるか，何れか其一に居らざるを得ず．上文に所謂，直線を兩分する點とは之を云ふなり．

直線に此の如き兩斷を施こし得べきことは，何人も首肯する所なるべし，然れども「我讀者の多數は連續の秘密が平凡此の如きに過ぎずと，聽きて意外の感に打たるゝならん」とはデヾキンドの危惧せる所なりき．彼は更に語を繼ぎて言へらく，「人若し上文の原則を明白にして，少しも直線なるものに對する自家の所觀に悖る所なしとなさば，我が幸之に過ぎず．如何にとならば予は此の原則の果して正當なるや否やを證明すること能はず，而も是れ何人と雖，成し得べからざる事に屬すればなり」と．讀者請ふ深く此語を翫味せよ．若し或は此原則の正否を論證せんと欲する誘惑を感ぜば，先づ抑〻證明とは如何なる事なるかを想へ．證明なきは能はざるに非ず，能ふ可らざるなり．

デヾキンドの法則に準據して，一の有理區域が果して凡ての量を網羅せりや否やを批判するときは最透徹せる解答を得．

一の有理區域に屬せる凡ての量を兩分して之を甲乙の二群となし，甲の量をして盡く乙の量より小ならしめ，而も甲に最大の量なく，乙に最小の量なからしむるを得べきことは，旣に說きたる所なり．然るに凡ての量の範圍內に於ては，斯の如き兩分に伴ひて必ず甲に最大の量あるか又は乙に最小の量あるを要するが故に，一の有理區域以外に尙ほ量なきを得ず．

デヾキンドの法則に於ける第三條件と（七）の切斷の第三條件と正反對なること，實に問題の要點なり．

分布の稠密なること，等分の可能なること，此等は凡て量の連續に關せる性質にして而も未だ連續の特徵を盡さず．此等の事實は實際盡く連續の法則の中に含蓄せらるゝこと，後章に至て自ら明白なるべし．

（九）

凡ての量に數値を與へんと欲せば，有理數のみを以て之を辨ずべからず．是に於て有理數以外新に數を作るの必要を生ず．斯の新數は卽ち無理數なり．

所謂抽象的の量と，有理無理のあらゆる數（正數）とは，其內容に於て異なる所あるべからず．數はよく凡ての量の數値を供給すべし．

然れども吾人は又凡ての量に數値を與ふべしとの此要求を充實せる上，更に一步を進めて量の數値たり得ざる數をも考へ得べき自由を有すること論なし．例へば $0$ の如し，量の本來の觀念に固着するときは， $0$ は量の數値として用なき數なり．然れども數の系統の統一及び其の法則の調和の爲には $0$ は缺くべからず．

個々の量と一直線上の個々の點とを對照せしむるときは（前節の圖を看よ）直線上の各〻の點は必ず或量を代表せり．唯其左端の一點 $O$ は則ち然らず．直線上の各〻の點を其代表せる量の數値に對照すれば，個々の點は個々の數に配合せらる，零なる數は $O$ なる點に配合せらるゝものと考ふることを得べし．

抽象的量の性質は又數の盡く具ふる所なり， $0$ を包括せる數の範圍內に於て次の諸原則成立す．

第一，二つの數は比較し得べし，其の結果は相等，大小の三者を出でず．數に一個最小の者あり， $0$ 卽ち是なり．

第二，數には組み合はせ及び交換の法則に遵へる加法を施すことを得，其結果唯一なり． $0$ の加法は $a + 0 = a$ によりて定まり，加法と大小との關係は $b > b^{'}$ と $a + b > a + b^{'}$ との相隨伴すべしといふに盡く．加法の轉倒（減法）は其可能なる限り，唯一の結果を與ふ．

第三，數の全範圍に連續あり．卽ち凡ての數を $𝐎$ ， $𝐔$ の二群に分ち， $𝐎$ に屬する數をして凡て $𝐔$ に屬する數より大ならしむるときは， $𝐎$ に最小の數あるか，或は $𝐔$ に最大の數あるか，二者いづれか其一に居らざるを得ず．

吾人は連續の法則を基礎として，次章に於て無理數の性質を闡明せんとす．上文擧ぐる所の原則は，完全に數の觀念を定むるものにして，此意義に於て，實に「數」の定義なりといふべし．第三章に於て整數の諸性質を根本的の原則より演釋せると同一の順序によりて，上述の諸原則より一般の數の諸性質を秩序的に導き出さんことは，蓋し數學に於て論理の嚴密を愛好する讀者の最も趣味あるを覺ゆべき問題なり．然れども吾人は後條に於て唯連續といふことの意義の實質的に確實に了解せられんことを期望するに止まり，卽ち問題の最重要なる一點を解釋して，其他は之を餘裕ある讀者の敷衍に一任せんと欲す．