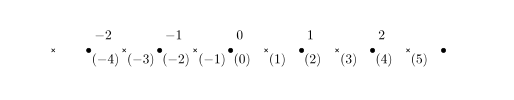第五章 分數
分數班の構成,分數班內の相等大小及加法減法,整數と分數班との內容の一致○通分,一般分數の相等大小及加法減法,旣約分數○分數班の總括,數の新系統,其特徵,分布の稠密なること及等分の可能○倍加及等分,最小公倍數及最大公約數○分數の比,比例式,分數の乘法,除法
(一)
分數の起源は量を計るにあり.然れども吾輩は姑らく此事實を度外に置き,此處には先づ順序の思想を根據として分數の觀念に到達せんとす.是れ一には汎く知られざる立脚點を紹介するの意に出で,又一には,負數の條に言へるが如く,數學上の觀念に具體的の內容を與ふることの,樣々になされ得べきを例證せんと欲するに由れり.
順序數の冒頭  を添へ,更に又
を添へ,更に又  に先ちて,逆に究なく連亙せる負數を附加して數の範圍を擴張することを得たり.今同一の思想を敷衍して,更に此方向に一步を進めんとす.
に先ちて,逆に究なく連亙せる負數を附加して數の範圍を擴張することを得たり.今同一の思想を敷衍して,更に此方向に一步を進めんとす.
先づ順逆兩面に亙りて究る所なき,物の引續きを考へ,此等の物の中任意に或一つを採りて,之を  と名づけ,(此物に
と名づけ,(此物に  を配合し)之に先後せる凡ての物に順次凡ての正及負の整數を配合すべし.此等の物の各には,直に之に次げる唯一個の物あり,斯の如く相隣接せる二つの物の中間に更に一個づゝ新しき物を插入せりとし,さて此等新舊兩種の物を一括して考ふるに,是亦順逆の兩方面に亙りて究る所なき,物の引き續きにして,此等凡てにも亦其順序に從ひて凡ての正及負の整數を配合することを得.若先に
を配合し)之に先後せる凡ての物に順次凡ての正及負の整數を配合すべし.此等の物の各には,直に之に次げる唯一個の物あり,斯の如く相隣接せる二つの物の中間に更に一個づゝ新しき物を插入せりとし,さて此等新舊兩種の物を一括して考ふるに,是亦順逆の兩方面に亙りて究る所なき,物の引き續きにして,此等凡てにも亦其順序に從ひて凡ての正及負の整數を配合することを得.若先に  を配合せる物には此度も亦
を配合せる物には此度も亦  を配合せりとし,且前後兩囘の配合を區別せん爲に,後に配合せる數を包むに括弧を以てするときは,此兩囘の配合は次の如き形貌を呈すべし.
を配合せりとし,且前後兩囘の配合を區別せん爲に,後に配合せる數を包むに括弧を以てするときは,此兩囘の配合は次の如き形貌を呈すべし.
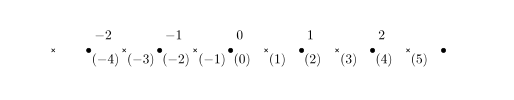
同一の物に二樣の命名をなし,一たびは其凡てに命名し,又一たびは其一半に命名して他の一半の命名を闕けり.一半には二樣の命名ありて,一半には唯一樣の命名あり.二樣の名稱の同一の物に屬せるを表はすに次の記法を用ゐるべし.(上の圖式を看よ)

一般に

不等の符號  ,
, は先後を表はすものとなして,例へば
は先後を表はすものとなして,例へば
(1)

など書く,一般に

或は物の異同にのみ着目して,名稱の新舊を問はずば
(2)

物の順序定まりたる上は第三章(二)の I,II によりて加法の意義を定むることを得,しかするときは例へば

一般に
(3)

こは直に  に次げる物は
に次げる物は  と言ふに同じ.例へば前の圖式に於て直に
と言ふに同じ.例へば前の圖式に於て直に  に次げるは
に次げるは  にして,又直に
にして,又直に  に次げるは
に次げるは  なり.
なり.
 を
を  の二倍と名づくれば,一般に
の二倍と名づくれば,一般に
(4)

の二倍は

なり.
若し又當初隣接せる二個の物の中間に  個づゝの新しき物を插入し,前の如く二樣の命名をなし,此度の新名稱をば,特に此
個づゝの新しき物を插入し,前の如く二樣の命名をなし,此度の新名稱をば,特に此  を添へたる記法にて書き表はさば,次の圖式を得.先に
を添へたる記法にて書き表はさば,次の圖式を得.先に  と書けるは此記法に從はば
と書けるは此記法に從はば  となすべきものなり.
となすべきものなり.

前と同樣に,一般に
(1*)

(2*)

(3*)


又  倍といふ語を前の如き意義に用ふれば,
倍といふ語を前の如き意義に用ふれば,
(4*)

の

倍は

なり.
隣接せる整數の間に  個づゝの新しき數を插入して數の範圍を擴張し,
個づゝの新しき數を插入して數の範圍を擴張し, の如き記法を以て此等の數を表して其大小の順序を明にし,又
の如き記法を以て此等の數を表して其大小の順序を明にし,又
I

II

によりて其加法を定む.(第三章(二)を參照せよ)又整數  は新範圍の一員として (1*) の名稱を得たりとす.(2*),(3*),(4*) は此等の規定の中に含まれたり.
は新範圍の一員として (1*) の名稱を得たりとす.(2*),(3*),(4*) は此等の規定の中に含まれたり.
 の如き記法はこと〴〵し,代ふるに
の如き記法はこと〴〵し,代ふるに  を以てすべし.
を以てすべし. は自然數にして
は自然數にして  は正又は負の整數(又は
は正又は負の整數(又は  )なり.斯の如き數を分數といひ,
)なり.斯の如き數を分數といひ, を其分母,
を其分母, を其分子といふ.分母,分子を分數の兩項となす.
を其分子といふ.分母,分子を分數の兩項となす.
 を
を  となすは,隣接せる整數の中間に新しき數を插入することなきの謂なりとなし,整數
となすは,隣接せる整數の中間に新しき數を插入することなきの謂なりとなし,整數  を分母
を分母  なる分數と呼びて用語上の便利を享ること大なり.同一の分母
なる分數と呼びて用語上の便利を享ること大なり.同一の分母  に屬せる分數を總括して假に之を分數班といふ,一の分數班の範圍內に於ける大小の關係及加法減法は次の如し.
に屬せる分數を總括して假に之を分數班といふ,一の分數班の範圍內に於ける大小の關係及加法減法は次の如し.
一,

と共に

二,

と共に

特に





要するに同一の分母  に屬せる分數の大小の關係及加減の算法は,其分子のそれぞれと全く同一に歸す.分數班は其一部として凡ての整數を包括せるが故に,其範圍整數のそれよりも廣大なるの觀ありと雖,實は兩者其內容を同じくして,唯個々の數の名稱に異同あるに過ぎず.
に屬せる分數の大小の關係及加減の算法は,其分子のそれぞれと全く同一に歸す.分數班は其一部として凡ての整數を包括せるが故に,其範圍整數のそれよりも廣大なるの觀ありと雖,實は兩者其內容を同じくして,唯個々の數の名稱に異同あるに過ぎず.
分母  なる分數班の中にありて,
なる分數班の中にありて, は整數の範圍內に於ける
は整數の範圍內に於ける  と同樣の位置を占めたり.
と同樣の位置を占めたり. を此分數班の單位或は幹分數といふ.
を此分數班の單位或は幹分數といふ.
(二)
今  と置き,分母
と置き,分母  に屬せる分數の中其分子が
に屬せる分數の中其分子が  の倍數なるもののみを保留して,其他を排斥するときは,
の倍數なるもののみを保留して,其他を排斥するときは,
(A)

を得,此等の數は又順逆兩面に亙りて究りなく連續し,而も其大小の關係及加法は全く分母  に屬せる凡ての分數のそれと異ならず.先づ隣接せる二つの整數
に屬せる凡ての分數のそれと異ならず.先づ隣接せる二つの整數  ,
, の中間には (A) の數恰も
の中間には (A) の數恰も  個の橫はれるを見る,
個の橫はれるを見る,

是なり.又

と共に


と共に

(A) の諸數と,分母  に屬せる分數
に屬せる分數
(B)

とは其成立の由來を外にして之を區別する所以の者全く有ることなし.是故に吾輩は (A),(B) を同一視して一般に

と置き,以て分母  に屬せる分數を分母
に屬せる分數を分母  に屬せる分數班の中に包括せしむ.分母に屬せる分數班は其一部として
に屬せる分數班の中に包括せしむ.分母に屬せる分數班は其一部として  の或約數を分母とせる分數を含蓄す.同一の分數は種々の分母に屬せる分數の中に包括せられ,此等の分數班の一員として種々の形式に表はさるゝことを得.
の或約數を分母とせる分數を含蓄す.同一の分數は種々の分母に屬せる分數の中に包括せられ,此等の分數班の一員として種々の形式に表はさるゝことを得.
 ,
, の公倍數の一つを
の公倍數の一つを  となせば,分母
となせば,分母  に屬する分數及分母
に屬する分數及分母  に屬する分數は共に盡く分母
に屬する分數は共に盡く分母  なる分數班の中に含蓄せられたり.今
なる分數班の中に含蓄せられたり.今

と置かば

 ,
, を分母
を分母  に屬せる分數班の一員として,其大小を比較し又之に加法減法を施こすことを得,卽ち
に屬せる分數班の一員として,其大小を比較し又之に加法減法を施こすことを得,卽ち

に伴ひて


然れども之を以て分數の大小及加法減法の定義となさんと欲せば,斯の如くにして定められたる大小の關係及加法減法の結果が公分母  の選擇に關係なきことを確めざるべからず.
の選擇に關係なきことを確めざるべからず.
相等及大小. ,
, の相等大小は
の相等大小は  ,
, の相等大小に隨件す.さて
の相等大小に隨件す.さて  に伴ひて
に伴ひて  (
( ,
, は共に自然數隨て正數なることを記憶すべし)
は共に自然數隨て正數なることを記憶すべし)  ,
, によりて,
によりて, 斯の如く
斯の如く  ,
, の相等大小は必ず
の相等大小は必ず  ,
, の相等大小と相伴ふにより,
の相等大小と相伴ふにより, ,
, の相等大小を判定するには,
の相等大小を判定するには, ,
, を比較せば則ち足る.さて
を比較せば則ち足る.さて  ,
, に
に  の痕跡なきにより
の痕跡なきにより  ,
, の相等大小は
の相等大小は  ,
, の公倍數
の公倍數  の選擇に關係なし.二つの分數を如何なる分數班に屬せるものとして其大小を比較するとも,其結果は恆に同じ.
の選擇に關係なし.二つの分數を如何なる分數班に屬せるものとして其大小を比較するとも,其結果は恆に同じ.
上述の說明の中より特に次の法則を採り出すべし.
 と
と  とは相伴ふ.
とは相伴ふ.
加法及減法.二つの分數  ,
, に同一の分母を與へて
に同一の分母を與へて

と置き,

によりて其和を定むるとき,此和は公分母  の選擇に關係なきを確めざるべからず.今公分母
の選擇に關係なきを確めざるべからず.今公分母  に代ふるに
に代ふるに  を以てし,更に
を以てし,更に

と置けば,先づ

より


より

を得,之を加へて

隨て

なるを知る.減法の場合も亦同じ.
是によりて分數の大小及加減を含める算式は,此等の分數を之に等しき他の分數を以て置き換へたるが爲に,其成立を妨げらるゝことなきを覺るべし.分數の加法が組み合はせの法則及交換の法則に遵ふこと明白なり,又整數の加法減法に關して第三章に述べたる事實は語句の更むべきを更めて,汎く之を分數に適用することを得.此處に此等の事實を證明する方法の一例として加法の交換の法則を證せんとす.
 ,
, が二つの分數なるとき
が二つの分數なるとき  なるを證せんことを要す.
なるを證せんことを要す. ,
, を公分母に直して
を公分母に直して  ,
, と置けば
と置けば

を得,整數  ,
, の加法には交換の法則を適用し得べきが故に,
の加法には交換の法則を適用し得べきが故に, 隨て
隨て  .
.
(三)
相等しき分數を總括して之を唯一つの數となし,卽ち分數の値に着目して分數の形式の異同を度外に置き,さて凡ての分數を打して一團となし,新に數の一系統を組織するときは,此範圍內に於て,二つの異なる(値の異なる)數の中唯一つが他の一よりも大にして,且大小なる語の意義は,よく自然數の場合に於て第一章(二)にいへるが如き條件に遵へり.又二つの數は必ず一定の和を有し,減法は凡ての場合に可能にして恆に一定の結果を與へ,且加法,減法は整數の場合と同一の性質を具へたり.
斯の如くにして作り出せる數の系統は,特別の場合として凡ての整數を含蓄せり.而して此新系統が啻に形式の上のみならず,內容に於て,實際整數の系統よりも廣大なる一範圍を成せることは,次の二つの事實の明に示す所なり.
一,分數の分布は各處稠密なり.凡て整數には必ず直に之より大又は小なる他の整數あり.相隣接せる整數の中間に第三の整數あるを許さず.整數に異樣の命名をなせるに過ぎずして,其內容の擴張にはあらざる,彼分數班なるものの範圍內に於ても,亦同樣の事實成立せり.然れども凡ての分數班を合同して作り成せる吾輩の新系統の範圍に於ては則ち然らず.
如何なる分數を考ふとも直に之より大又は小なりと云ひ得べき分數存在することなし,相隣接せる二個の分數は不可有なり.相異なる二つの分數の中間に必ず第三の分數存在す.詳しく言はゞ  ,
, が相異なる分數にして,例へば
が相異なる分數にして,例へば  なるときは,
なるときは, なる如き分數
なる如き分數  は必ず存在す.此事實は直に證明せらるべし,姑らく此事成立せりとなさんに
は必ず存在す.此事實は直に證明せらるべし,姑らく此事成立せりとなさんに  は亦
は亦  と異なるが故に,
と異なるが故に, ,
, の中間に
の中間に  なる分數
なる分數  ,又
,又  ,
, の中間に
の中間に  なる分數
なる分數  存在し,
存在し, ,
, ,
, はいづれも
はいづれも  ,
, の中間に橫はるが故に,斯の如くにして,相異なる二つの分數の中間には限りなく多くの分數を容るを知るべし.分數の分布各處稠密なりといへるは此意なり.
の中間に橫はるが故に,斯の如くにして,相異なる二つの分數の中間には限りなく多くの分數を容るを知るべし.分數の分布各處稠密なりといへるは此意なり.
 ,
, が相異なる分數にして
が相異なる分數にして  ならば,
ならば, ,
, を同分母の分數となして
を同分母の分數となして

と置くとき  にして
にして  ,
, は整數なるが故に
は整數なるが故に  ,
, の差は少くとも
の差は少くとも  に等し.
に等し. ,
, の差
の差  より大ならば,
より大ならば, ,
, の中間に橫はれる整數あり,其一つを
の中間に橫はれる整數あり,其一つを  と名づけ,
と名づけ, を採らば
を採らば  又若
又若  ,
, の差
の差  に等しからば
に等しからば  を
を  より大なる自然數となし
より大なる自然數となし

となすとき  と
と  との差は
との差は  よりも大なり.是故に如何なる場合にも
よりも大なり.是故に如何なる場合にも  ,
, の中間には必ず第三の分數
の中間には必ず第三の分數  の存在するを知るべし.
の存在するを知るべし.
二,等分の可能. を以て一の自然數を表はすとき,
を以て一の自然數を表はすとき, なる數
なる數  個の和を
個の和を  の
の  倍といふ,
倍といふ, の
の  倍は
倍は  と同一分數班の中に於て之を求め得べし.
と同一分數班の中に於て之を求め得べし. が
が  の
の  倍に等しといふことを
倍に等しといふことを


と書く.今  及
及  が與へられたりとして,
が與へられたりとして, を求めんとするに,
を求めんとするに, は必しも
は必しも  と同一の分數班の中に存在せず.例へばある整數を
と同一の分數班の中に存在せず.例へばある整數を  等分することは必しも整數の範圍內に於てなさるべくもあらず.然れども凡ての分數を包括せる數の新系統の範圍內にありては,等分は凡ての場合に可能なり.げにも今
等分することは必しも整數の範圍內に於てなさるべくもあらず.然れども凡ての分數を包括せる數の新系統の範圍內にありては,等分は凡ての場合に可能なり.げにも今

と置かば

は明に上の條件に適せり.
稠密なる分布,及等分の可能は整數に缺如せる所にして,此二條件は凡ての分數より成立せる數の新範圍が內容の上に於て,果して整數のそれよりも廣大なるを證する著明なる特徵なりといふべし.
此處に於て,尙分數の標準形式につきて一言するの機會を逸すべからず.凡て分數は之を限りなく多くの相異なる形式に表はし得べきことは旣に說きたり. なる分數の與へられたるときは,
なる分數の與へられたるときは, を如何なる(正の)整數となすとも,恆に
を如何なる(正の)整數となすとも,恆に

なることは前節に說きたる分數相等の照準によりて明白なり.此等式を順に又逆に讀むときは,凡て分數の分母及分子に同一の自然數を乘じ,又は分母及分子を其公約數  にて除して得らるべき分數は原分數に等しきを知るべし.今
にて除して得らるべき分數は原分數に等しきを知るべし.今  ,
, を其最大公約數にて除し
を其最大公約數にて除し

を得たりとせば, ,
, は相素なる整數なり,斯の如く分母と分子とに公約數なき分數を旣約分數と云ふ.凡て分數は之を「旣約分數に直す」ことを得.旣約分數とは特殊なる分數にあらずして,分數の特殊なる形式なり.
は相素なる整數なり,斯の如く分母と分子とに公約數なき分數を旣約分數と云ふ.凡て分數は之を「旣約分數に直す」ことを得.旣約分數とは特殊なる分數にあらずして,分數の特殊なる形式なり.
又逆に  なる分數が
なる分數が  なる旣約分數に等しきときは,
なる旣約分數に等しきときは, 及
及  はそれそれ
はそれそれ  及
及  の同係數の倍數なり.げにも
の同係數の倍數なり.げにも

より

を得,此等式は  の
の  の倍數なるべきを示せり.さて
の倍數なるべきを示せり.さて  は
は  と相素なるが故に第四章(五)によりて
と相素なるが故に第四章(五)によりて  は
は  の倍數ならざるを得ず,今
の倍數ならざるを得ず,今  と置かば上の等式より
と置かば上の等式より  を得べきなり.
を得べきなり.
是故に旣約分數は,ある分數の有し得べき種々の形式の中最小の分母を有せるものなり.二個の旣約分數の相等しきは其分母及分子各相等しき場合に限る.
(四)
 を分數,
を分數, を自然數とするとき,
を自然數とするとき, なる數
なる數  個の和を
個の和を  の
の  倍といひ,之を表すに
倍といひ,之を表すに  なる記法を以てせり.此定義は
なる記法を以てせり.此定義は  の
の  より大なるべきを豫想す,今
より大なるべきを豫想す,今  ,
, によりて此定義を
によりて此定義を  が正又は負の任意の整數なる場合に擴充し,
が正又は負の任意の整數なる場合に擴充し, なるとき
なるとき  を
を  の倍數,
の倍數, を
を  の約數と稱す.
の約數と稱す. の倍數に關する次の諸定理は容易に證明し得べき所なり.
の倍數に關する次の諸定理は容易に證明し得べき所なり.



 なるは
なるは  又は
又は  なるときに限る,
なるときに限る, は
は  の
の  に等しからざる限り必ず
に等しからざる限り必ず  に伴ひ,又
に伴ひ,又  は
は  の
の  ならざる上は必ず
ならざる上は必ず  に伴ふ.
に伴ふ.
 の等分は恆に可能にして且一定の結果を與ふ.
の等分は恆に可能にして且一定の結果を與ふ. なる條件に適すべき數
なる條件に適すべき數  を表はすに分數の記法を襲用して
を表はすに分數の記法を襲用して  となす.
となす. なる分數の
なる分數の  倍は
倍は  に等し.よりて分數の分母は必ず正の整數なるべしとの制限を撤去し,一般に
に等し.よりて分數の分母は必ず正の整數なるべしとの制限を撤去し,一般に

となして記法の變通を許すべし.
 は
は  の
の  ならざる限り必ず
ならざる限り必ず  に伴ふ.
に伴ふ. は
は  の
の  ならざるときに限り意義を有し,恆に
ならざるときに限り意義を有し,恆に  に伴ふ.
に伴ふ.
倍加と等分とを引續き適用する場合に,其順序は最終の結果に影響することなし.卽ち

 とは等分の記法の定義によりて
とは等分の記法の定義によりて  の
の  倍を
倍を  分して得らるべき數にして,
分して得らるべき數にして, とは
とは  を
を  分して得たる數の
分して得たる數の  倍なり.此二つの數の相等しきを確めんが爲に其
倍なり.此二つの數の相等しきを確めんが爲に其  倍を比較すべし.
倍を比較すべし. の
の  倍は卽ち
倍は卽ち  にして,又
にして,又  の
の  倍卽ち
倍卽ち  は
は  なり.此相等しき數を表はすに
なり.此相等しき數を表はすに

なる記法を以てす.
今  ,
, 等を以て一般に
等を以て一般に  の如き分數を表はすときは,
の如き分數を表はすときは, は
は  の
の  ならざる限り必ず
ならざる限り必ず  に伴ひ,又
に伴ひ,又  は
は  の
の  ならざる限り必ず
ならざる限り必ず  に
伴ふ,又
に
伴ふ,又


 ,
, が與へられたる分數にして
が與へられたる分數にして  が
が  に非ざるときは,
に非ざるときは, なる條件に適すべき分數
なる條件に適すべき分數  は必ず存在す.先づ
は必ず存在す.先づ  が
が  なるときは
なるときは  なり,又
なり,又  が
が  にあらざるときは
にあらざるときは  ,
, に分母を同じくせる形式を與へて
に分母を同じくせる形式を與へて

となし

を得.
斯くして定め得たる分數  を旣約分數に直して
を旣約分數に直して  を得たりとせば
を得たりとせば

にして之を
(1)

なる形に書き改むることを得.
 は
は  及
及  の約數にして,
の約數にして, 及
及  の公約數は必ず
の公約數は必ず  の約數なり.げにも今
の約數なり.げにも今  を
を  ,
, の公約數の一となし
の公約數の一となし

となさば,之を (1) より得らるべき

と組み合はせて

を得,隨て

にして  ,
, は公約數なき整數なるが故に,屢〻用ゐたる論法によりて
は公約數なき整數なるが故に,屢〻用ゐたる論法によりて

なる如き整數  の存在すべきを知り
の存在すべきを知り

を得,隨て

を知る, は
は  の約數なり.
の約數なり. を
を  ,
, の最大公約數と云ふ.最大の語は値の大小に關係なく,單に
の最大公約數と云ふ.最大の語は値の大小に關係なく,單に  ,
, の公約數は盡く
の公約數は盡く  の約數なるを示せる形容詞なりと認めて可なり.實際
の約數なるを示せる形容詞なりと認めて可なり.實際  に於て最大なるは
に於て最大なるは  ,
, の公約數の絕對値なり.然れども大小の關係はこゝに樞要の意義を有せるに非ず.
の公約數の絕對値なり.然れども大小の關係はこゝに樞要の意義を有せるに非ず.
又  は
は  及
及  の倍數にして,
の倍數にして, ,
, の公倍數は必ず
の公倍數は必ず  の倍數なり.此意義に於て
の倍數なり.此意義に於て  を
を  ,
, の最大公倍數といふ.げにも
の最大公倍數といふ.げにも  を
を  ,
, の公倍數の一となし
の公倍數の一となし

と置けば

によりて定めらるゝ  は
は  ,
, の公約數,隨て
の公約數,隨て  の約數なり.今
の約數なり.今

となさば,(1) の  より
より

隨て又

を得,これより

を得  は
は  の倍數なり.
の倍數なり.
斯の如くにして,最大公約數及最小公倍數の觀念を分數の上に擴張することを得たり.二つの整數の最大公約數が  なるとき此二つの整數を相素なりといへる稱呼は之れを分數の場合に襲用せんこと無用なり.二つの分數は限りなく多くの公約數を有す.
なるとき此二つの整數を相素なりといへる稱呼は之れを分數の場合に襲用せんこと無用なり.二つの分數は限りなく多くの公約數を有す.
例へば  ,
, となさば
となさば

にして

なり.又  ,
, とせば
とせば  にして,凡て
にして,凡て  を分子とせる分數は盡く
を分子とせる分數は盡く  ,
, の公約數なり.
の公約數なり.
(五)
倍數及約數なる語によりて言ひ表はされたる,二數の關係を擴張して,比の觀念を得. ,
, の最大公約數を
の最大公約數を  とし
とし  ,
, と置き,符號の不定を避けんが爲に
と置き,符號の不定を避けんが爲に  を正となす如く
を正となす如く  の符號を定むるものとせば斯の如くにして
の符號を定むるものとせば斯の如くにして  ,
, なる二つの與へられたる數より一定の相素なる一對の整數
なる二つの與へられたる數より一定の相素なる一對の整數  ,
, を得.さて此手續きによりて
を得.さて此手續きによりて  ,
, より同一の整數
より同一の整數  ,
, の導き出さるゝときは,
の導き出さるゝときは, ,
, の比と
の比と  ,
, との比相等しと稱し,之を書き表すに
との比相等しと稱し,之を書き表すに

なる記法を以てす.此意義に從て

同一の比に等しき二つの比は亦相等し. が既約分數なるときは
が既約分數なるときは  と
と  との最大公約數は
との最大公約數は  に等しく
に等しく

なり.是故に凡て二つの數の此は或定まれる相素なる一對の整數の比に等しく,又或定まれる分數と  との比に等し.
との比に等し.
此一定の分數  を
を  なる比の値と稱す.相等しき比は同一の値を有し,同一の値を有する比は相等し.向後思想の紛亂の虞なきこと明なる場合には比の値といふべきを略して單に比といふことあるべし.
なる比の値と稱す.相等しき比は同一の値を有し,同一の値を有する比は相等し.向後思想の紛亂の虞なきこと明なる場合には比の値といふべきを略して單に比といふことあるべし.
 なる比の値
なる比の値  なりといふことを書き表はすに
なりといふことを書き表はすに

なる記法を用ゐる,此場合には前節に說きたる意義に從ひて

なり.例へば


 ,
, を一般に二つの數,
を一般に二つの數, ,
, を二つの整數となすときは
を二つの整數となすときは
(1)

,(2)

,(3)

,(4)

はいづれも同一の事實を表はせり.
二つの此の相等しきを表はせる等式を比例式といふ.

なる比冽式成立するときは, ,
, ,
, ,
, は比例を成せりといふ.
は比例を成せりといふ. ,
, ,
, ,
, なる四つの數比例を成せるときは,其中三つの與へらるゝとき,第四の者は自ら定まる.此第四者を定むるを比例を解くといふ.
なる四つの數比例を成せるときは,其中三つの與へらるゝとき,第四の者は自ら定まる.此第四者を定むるを比例を解くといふ.
比例を成せる四つの數の中,三つの與へられるは卽ち相等しかるべき二つの比の中の一つと,他の一つの比の兩項の中一つとが與へられたるなり.是故に比例を解くとは, の與へられたるとき
の與へられたるとき

又は

なる比の値を與へられたる數に等しからしむべく  を定むるに外ならず.此與へられたる値を
を定むるに外ならず.此與へられたる値を  となし
となし

なるべきを要求するは,畢竟

なる條件により  を定めんとするなり.是故に
を定めんとするなり.是故に  なり.
なり. の場合も亦同樣なり.
の場合も亦同樣なり.
 ,
, を與へて
を與へて  の値を求むるは
の値を求むるは

を解きて  を定むるに外ならず.
を定むるに外ならず.
 の値が整數
の値が整數  に等しきときは
に等しきときは  は
は  の
の  倍なり.此場合に
倍なり.此場合に  の値を求むるは
の値を求むるは  より
より  を定むることにして,是卽ち倍加の問題の轉倒なり.是故に吾輩は除法の意義を擴張して,
を定むることにして,是卽ち倍加の問題の轉倒なり.是故に吾輩は除法の意義を擴張して, ,
, より
より

なる條件に適すべき數  を定むる算法を分數の除法と名づけんとす.實,法,商の語又此場合に襲用すべし.分數除法は法が
を定むる算法を分數の除法と名づけんとす.實,法,商の語又此場合に襲用すべし.分數除法は法が  ならざる限り,凡ての場合に可能にして常に唯一の結果を與ふ,又特別の場合に於て實及法が共に整數にして實が法の倍數なるときは,商は整數除法の商と異ならず.整數の除法はこゝに定めたる除法の特例たるに過ぎずと謂ふべし.
ならざる限り,凡ての場合に可能にして常に唯一の結果を與ふ,又特別の場合に於て實及法が共に整數にして實が法の倍數なるときは,商は整數除法の商と異ならず.整數の除法はこゝに定めたる除法の特例たるに過ぎずと謂ふべし.
此意義に從ふときは整數  を整數
を整數  にて除して得たる商は卽ち分數
にて除して得たる商は卽ち分數  なり.
なり.
整數  に整數
に整數  を乘ずるは,
を乘ずるは, より
より  を定むるに同じく,
を定むるに同じく, を
を  倍するは
倍するは  より
より  を定むるに異ならず.一般に
を定むるに異ならず.一般に  及
及  を與へて
を與へて

なる條件に適合すべき  を定むるは卽ち除法の轉倒にして,此算法は特別の場合として整數の乘法及一般に數の倍加を包括す.是故に此算法を仍乘法と名づけ,
を定むるは卽ち除法の轉倒にして,此算法は特別の場合として整數の乘法及一般に數の倍加を包括す.是故に此算法を仍乘法と名づけ, ,
, ,
, の關係を表すに
の關係を表すに

なる記法を以てす.因子及積の語又此場合に襲用すべし. に
に  を乘ずるは畢竟
を乘ずるは畢竟

なる比例式を解きて  を定むるに歸着し,
を定むるに歸着し, は
は  ,
, と共に全く定まる.
と共に全く定まる.
分數の乘法,除法は比例式解法の特例に過ぎず,其演算は次の如くにして整數の乘法及除法に歸着せしむることを得.
先づ

と置き  を解きて
を解きて  を求めん爲に,右邊の比を
を求めん爲に,右邊の比を  となして前節の比例解法を適用すれば
となして前節の比例解法を適用すれば

を得.此結果は分數乘法の組み合はせの法則及交換の法則に遵ふを明示するものなり.
加法減法に對する分配の法則も亦此結果を用ゐて容易に證明することを得,
今更に

と置けば

こゝに  の分母を
の分母を  の分母と同一となせるは,此法則の汎通を妨ぐるものにあらざるや明白なり.
の分母と同一となせるは,此法則の汎通を妨ぐるものにあらざるや明白なり.
乘法に於て因子の形式の異同は積に影響することなし,卽ち  ,
, ならば必ず
ならば必ず  なるべし.こは比の兩項を夫々之に等しき數を以て置き換ふるも比の値變することなしといへる事實の當然の結果なり.是故に
なるべし.こは比の兩項を夫々之に等しき數を以て置き換ふるも比の値變することなしといへる事實の當然の結果なり.是故に  より
より  を得.然れども又逆に
を得.然れども又逆に  なるときは必ず
なるときは必ず  なりといふことを得べし,げにも
なりといふことを得べし,げにも  ,
, にして
にして  は
は  に隨伴せざるを得ず.
に隨伴せざるを得ず. の
の  なる場合は例外なるを忘るゝことなかれ.
なる場合は例外なるを忘るゝことなかれ.
比例式の外項の積と內項の積とは相等し,卽ち

なるときは又

にして,且此二つは同一の關係なり.げにも先づ  なるとき此相等しき二つの比の値を
なるとき此相等しき二つの比の値を  と名づくれば
と名づくれば  ,
, よりて
よりて  乘法の組み合はせの法則により
乘法の組み合はせの法則により  隨て
隨て  .又逆に
.又逆に  なるときは
なるときは  の値を
の値を  と名づけ,
と名づけ, を得,隨て順次
を得,隨て順次  ,
, ,
, を經て
を經て  に達す.是故に
に達す.是故に

は必ず相隨伴す.
比の兩項に  と異なる同一の數を乘ずるも,比の値變することなし,卽ち
と異なる同一の數を乘ずるも,比の値變することなし,卽ち  げにも
げにも 
 ,
, なる二つの數は,
なる二つの數は, なる關係をなせり,而して此等式は
なる關係をなせり,而して此等式は  ,
, の中の一つと共に他の一つを定むるものなり,斯の如き二數
の中の一つと共に他の一つを定むるものなり,斯の如き二數  ,
, を互に逆なる數といふ.
を互に逆なる數といふ. ,
, が互に逆なる數なるときは
が互に逆なる數なるときは

なり.此結果を利用して

なるとき

を解きて  を求めんとするに,先づ
を求めんとするに,先づ  の逆數
の逆數  を採り之を左邊に立てる比の項に乘じて
を採り之を左邊に立てる比の項に乘じて  を獲,これより直に
を獲,これより直に  卽ち
卽ち

を得, を
を  にて除するは,
にて除するは, に
に  の逆數
の逆數  を乘ずるに異ならず.分數の範圍內にありては,乘法除法,其致一なり.
を乘ずるに異ならず.分數の範圍內にありては,乘法除法,其致一なり.
 ,
, の積は
の積は  の
の  に代入して此比例式を成立せしむべき數なりとの乘法の定義は一の缺陷を有す.そは
に代入して此比例式を成立せしむべき數なりとの乘法の定義は一の缺陷を有す.そは  の
の  なる場合に於て
なる場合に於て  なる比隨て
なる比隨て  の如き積の意義なきこと是なり.然れども
の如き積の意義なきこと是なり.然れども  の
の  なるときは
なるときは  より
より  を得べくして,乘法は一般に交換の法則に從ふが故に,
を得べくして,乘法は一般に交換の法則に從ふが故に, も亦
も亦  なるべしと定めて,此缺陷を補ふことを得べし.
なるべしと定めて,此缺陷を補ふことを得べし.
法の  なる除法に意義なきは勿論にして,此點につきて誤解あるべからず.
なる除法に意義なきは勿論にして,此點につきて誤解あるべからず.